fishingkasce.blogg.se - Ode45 matlab 2018b

The latter have special domains and center points of the form Taylor models of type 0 are the default, Taylor models of type 1 are used for solving ODEs. Ys_image = ys.image % enclosure of polynomial image p(D-c) ys = Ys_interval = ys.interval % error interval E Ys_coefficient = ys.coefficient % polynomial coefficients p Ys_monomial = ys.monomial % polynomial exponents Technically, the components of a Taylor model read as follows: ys = struct(y) Only for ease of presentation we chose the stated data with wide range. In practice, Taylor models with thin ranges of diameter much less than 1 are typical. The true range R = + E of y is very much overestimated by + E. _ _ _ _ _ _ _Ī quite large enclosure = of the polynomial image p(D-c) = p(D) = is computed automatically. Of degree d = 5, standard domain, standard center point, and error interval can be created as follows: p = % polynomial coefficientsĭim order type iv_mid iv_rad im_inf im_sup This is the big advantage of Taylor models: they allow to enclose higher dimensional shapes with curved boundaries without too much overestimation, see the pictures in Section "Taylor model arithmetic".Īs a first simple example, a Taylor model y with polynomial part This set R is not necessarily convex anymore. Taking a second Taylor model z = (q,D,c,F) with same domain and center point, the range R of the Taylor model vector w = (y,z) is defined by We remark that the polynomial coefficients p_a, the domain bounds u_i, v_i, and the center points c_i are restricted to be floating-point numbers in order to keep them representable on a computer.įor the single Taylor model y = (p,D,c,E) the range is a closed interval. Thus, the enclosure (range) represented by the Taylor model data p, D, c, E enlarges to Moreover, a Taylor model contains an error interval E which absorbs the inevitable rounding and degree truncation errors. For the special case of degree d = 1, standard domain Ds, and center point cs this coincides with the enclosure represented by an object in affine arithmetic with n error terms. Is the enclosure represented by the data p, D, and c. For example, c = u or c = v are also allowed, only c_i must be in. Next, a "center point" c = (c_1.,c_n) in D is fixed which must not necessarily be the exact center (u+v)/2.

Is fixed which is simply an interval vector of length n with interval components, i = 1.,n. Where a = (a_1.,a_n) is a multi index consisting of non negative integerĮxponents a_i and the polynomial coefficients p_a are real numbers.

Of bounded degree d in a fixed number of n variables. The simplest way is to think of a Taylor model as a multivariate, real polynomial p

Example VI - A Kepler problem for asteroid motion.

Example IV - The van der Pol equation, a second order ODE.

Example II - Lotka-Volterra equations, a two-dimensional ODE system.

ODE23/ODE45 are optimized for a variable step, run faster with a variable step size, and clearly the results are more accurate. Using a variable step ensures that a large step size is used for low frequencies and a small step size is used for high frequencies. Using an algorithm that uses a fixed step size is dangerous since you may miss points where your signal's frequency is greater than the solver's frequency. These integration methods do not lend themselves to a fixed step size. The way that ODE23 and ODE45 utilize these methods is by selecting a point, taking the derivative of the function at that point, checking to see if the value is greater than or less than the tolerance, and altering the step size accordingly. ODE23 is based on the integration method, Runge Kutta23, and ODE45 is based on the integration method, Runge Kutta45.

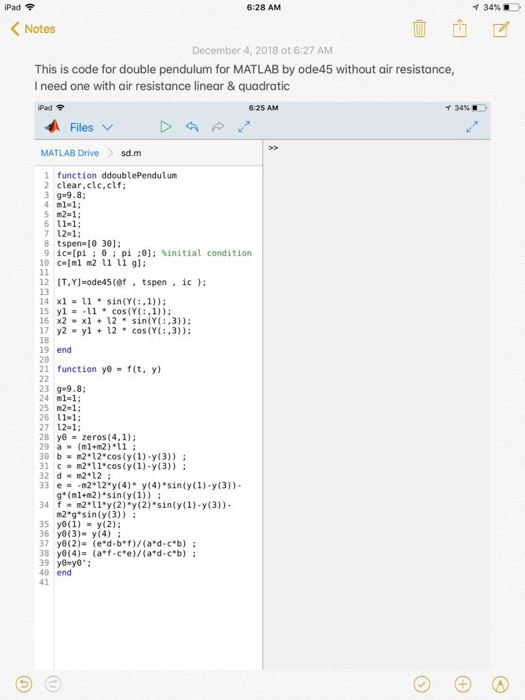
ODE23 and ODE45 are MATLAB's ordinary differential equation solver functions.